top

Documentation (OpenOCL v6)

In OpenOCL you can solve a large class of optimal control problems including non-linear, continuous-time, multi-stage, and constrained problems, which can appear in the context of trajectory optimization and model predictive control. The types of dynamical systems that are supported are all systems that can be described by ordinary differential equations or differential algebraic equations.

We introduced some new concepts that should make it as easy as possible for you to model optimal control problems, in particular the notion of grid-costs and grid-constraints that can be very handy when implementing tracking problems. In the following we give a short introduction to the concepts used and introduced in OpenOCL.

Cost terms and constraints

We support bounds that hold along the entire trajectory, and grid-constraints that hold only at specific gridpoints in the discretized trajectory.

For the cost terms you can specify path-costs that are integrated along the trajectory (also known as Lagrange term), and grid-costs that can be specified for specific points on the discretized trajectory.

Optimal control problem definition (single-stage)

For optimal control problems with a single stage, OpenOCL supports the following type of optimal control problems: where $x(t)$ is the state trajectory, $u(t)$ the control trajectory, $z(t)$ the algebraic state trajectory, $p$ the parameters, $l_p(x,z,u,p)$ the path cost function, $l_e(x,p)$ the terminal cost function, $f(x,z,u,p)$ the system dynamics function (differential equation), $g(x,z,u,p)$ the algebraic constraints function. The bounds on the variables are given by $x_\mathrm{0,lb}$, $x_\mathrm{0,ub}$ (initial state), $x_\mathrm{e,lb}$, $x_{e,ub}$ (end state), $x_\mathrm{lb}$, $x_\mathrm{ub}$, $z_\mathrm{lb}$, $z_\mathrm{ub}$, $u_\mathrm{lb}$, $u_\mathrm{ub}$.

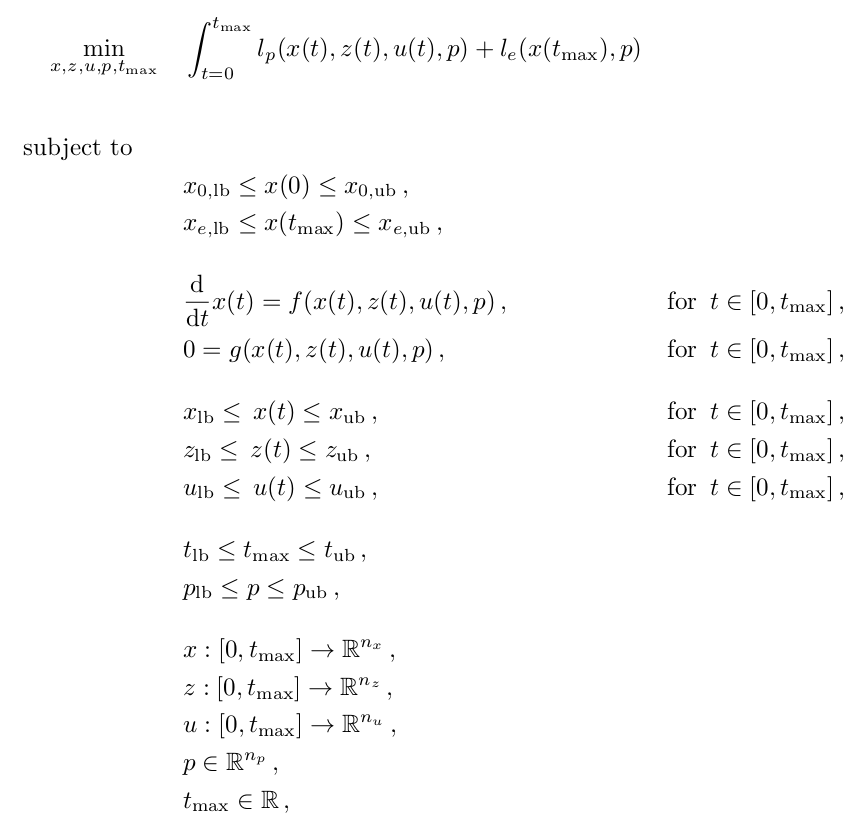
If no algebraic states $z$ are defined, the system is described by an ordinary differential equation. If algebraic states are defined, then the dynamics function $f(x,z,u,p)$ together with the algebraic constraints function $g(x,z,u,p)$ define the system dynamics as a differential algebraic equation in the semi-implicit form. To solve an optimal control problem, the index of the differential algebraic equation has to be smaller than or equal to one.

The dimension of the variables are: number of states $n_x$ , number of algebraic states $n_z$, number of controls $n_u$, number of parameters $n_p$.

ocl.Constraint()

Methods

ocl.Cost()

Methods

ocl.DaeHandler()

Methods

ocl.Simulator(vars, dae)

Arguments:

Returns:

Methods

ocl.Solver(T, vars, dae, pathcost, terminalcost)

function vanderpol
  solver = ocl.Solver(10, @varsfun, @daefun, @pathcost, 'N', 30);

  solver.setInitialBounds('x',     0);
  solver.setInitialBounds('y',     1);

  initialGuess = solver.getInitialGuess();
  initialGuess.states.x.set(-0.2);

  [solution,timepoints] = solver.solve(initialGuess);

  % plotting of control and state p trajectory:
  ocl.plot(timepoints.controls, solution.controls.u)
  ocl.plot(timepoints.states, solution.states.p)
end

function varsfun(vh)
  vh.addState('x', 'lb', -0.25, 'ub', inf);
  vh.addState('y');
  vh.addControl('F', 'lb', -1, 'ub', 1);
end

function daefun(daeh,x,~,u,~)
  daeh.setODE('x', (1-x.y^2)*x.x - x.y + u.F);
  daeh.setODE('y', x.x);
end

function pathcost(ch,x,~,u,~)
  ch.add( x.x^2 );
  ch.add( x.y^2 );
  ch.add( u.F^2 );
end

Arguments:

Returns:

Methods

ocl.Solver(stages, transitions)

Arguments:

Returns:

Methods

ocl.Stage(T, vars, dae, pathcosts)

stage = ocl.Stage([], @vars, @ode, 'N', 10, 'd', 2);

% Function definitions can be in the same file
% (if the main script is wrapped by a function)
% or in separate files:
function vars(sh)
  sh.addState('s');
  sh.addState('v');
end

function ode(sh,x,~,~,~)
  sh.setODE('s', x.v);
  sh.setODE('v', -10);
end

Arguments:

ocl.Variable()

% v is a solution of an OCP
% p=[px;py;pz] is of size 3x1
% p trajectory is of size 3x1x(N+1)
% F trajectory is of size 1x1xN
% with N control intervals
p = v.states.p;     % get state p trajectory
F = v.controls.F;   % get control F trajectory

% set all 3x1 p states to the same value
v.states.p = [3;2;1];
% set p states 4 and 5 in the trajectory
v.states.p(:,:,4:5) = [1,2,3;4,5,6].';
% or (with the same result)
v.states.p(:,:,4:5) = {[1;2;3],[4;5;6]};
% or even
v.states.p(:,:,4:5) = {[1,2,3],[4,5,6]};

% set all px values of p in state trajectory
v.states.p(1,:,:) = 4;

% plotting of state p trajectory:
plot(t.states.value,v.states.p.value)

Methods

Variable:
  Size: [3681 1]
  Type: OclStructure
  Children: states, integrator, controls, parameters, time
  Value: [100;2;1;0;0;0;0;0;0;0;0;0;0;0;0..]

ocl.VarsHandler()

Methods

@(ch, x, z, u, p)

Arguments:

@(daeh, x, z, u, p)

Arguments:

@(vh)

Arguments:

CasadiOptions()

casadi_options = struct;
casadi_options.ipopt = struct;
casadi_options.ipopt.linear_solver = 'mumps';
casadi_options.ipopt.hessian_approximation = 'exact';

Returns: